接下来就是残酷的淘汰赛。 16支球队谁会获胜？谁能夺得冠军？

今天3M小伙也来八卦一下：如何根据之前的小组赛预测出更科学、更靠谱的冠军结果？

1. 模拟方法

为了预测谁会获胜，我们首先要回顾一下淘汰赛的比赛规则。淘汰晋级图如下：

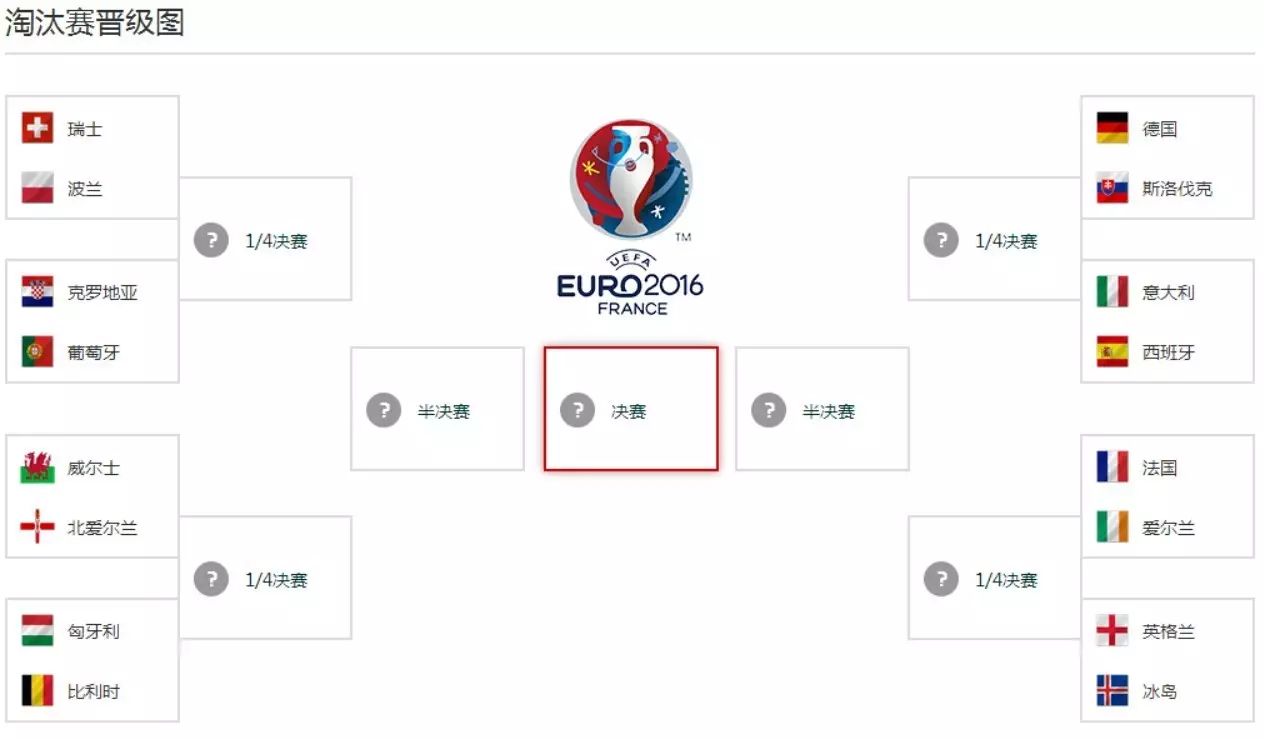
北京时间16强赛：

上半部分：

瑞士 vs 波兰（6月25日21:00）

克罗地亚 vs 葡萄牙（6 月 26 日 03:00）

威尔士 vs 北爱尔兰（6 月 26 日 00:00）

匈牙利 vs 比利时（6 月 27 日 03:00）

下半部分：

德国 vs 斯洛伐克（6 月 27 日 00:00）

意大利 vs 西班牙（6 月 28 日 00:00）

法国 vs 爱尔兰（6月26日21:00）

英格兰 vs 冰岛（6 月 28 日 03:00）

淘汰赛将16支球队分为8个小组，胜者晋级四分之一决赛。然后获胜的8支队伍被分为4组继续比赛，其中一半被淘汰，以此类推，直到获得冠军。

为了找出冠军是谁，需要模拟这个淘汰过程。为了模拟这个过程，需要预测每场比赛的结果。例如，首先需要模拟的是瑞士和波兰的比赛谁能获胜。

当两支球队竞争时，他们需要什么才能获胜？实力+运气。实力是指球队稳定运转时的表现水平，但一支球队的表现受到很多因素的影响（天气、伤病、心情、现场表现甚至球迷的喊声等），而这些因素是不可预测的。因素，俗称运气。

下图说明了力量的重要性。假设你和C罗各自带队参赛，而其他球员实力相当，那么你的球队很有可能会被C罗欺负。

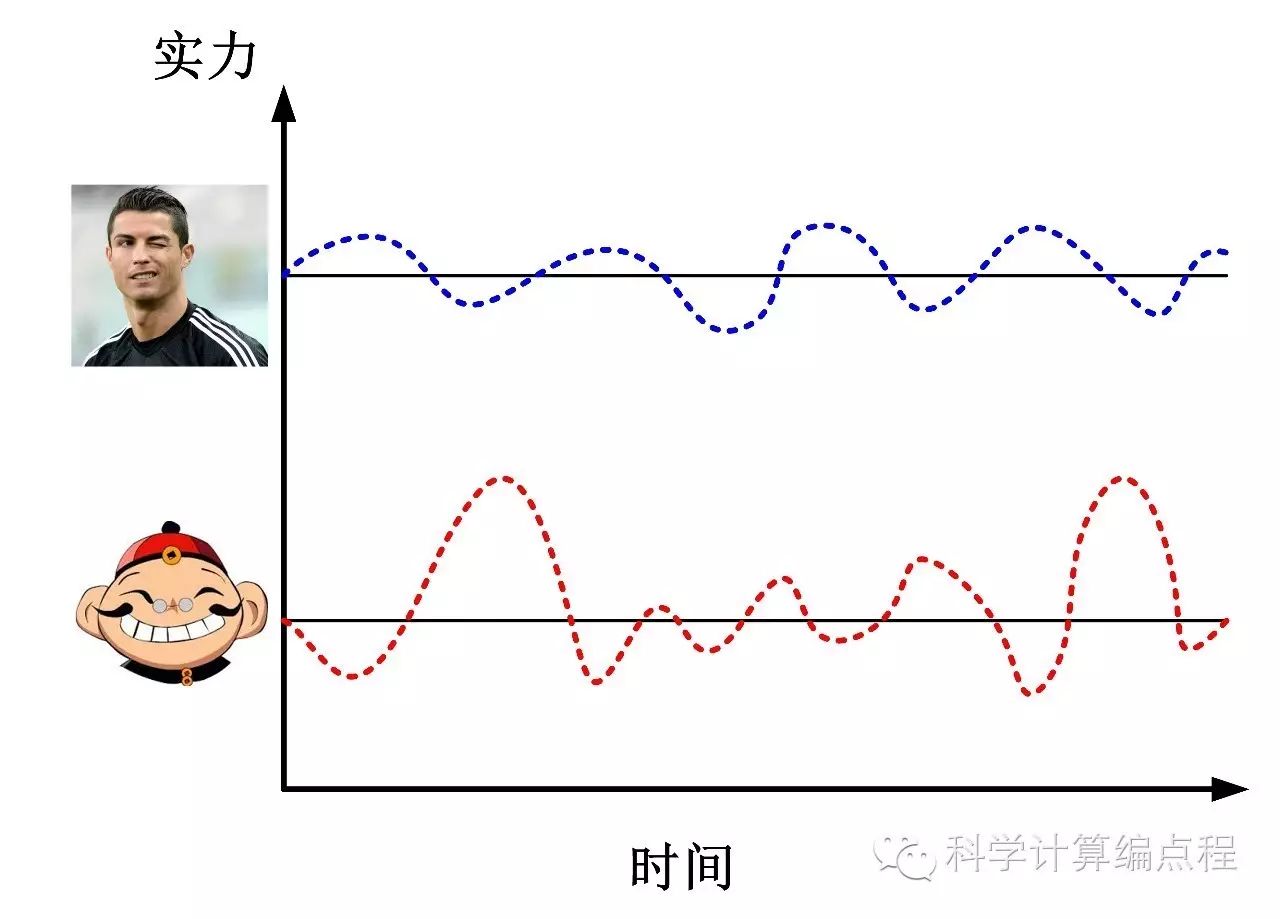
因为看上图，C罗的实力就是上面的黑线，而受到运气影响后的实际表现就是蓝色的虚线；你的实力是下面的黑线，受运气影响后的实际表现是红色虚线。

因为实力相差太大，就算你运气最好，C罗运气最差，你也赢不了他……

在绝对的实力差距面前，一切技巧都是徒劳。同样的原因也可以解释为什么日本在二战期间无法击败美国。穷二代追女孩很难和富二代竞争，小公司很难和大公司竞争。

然而，当实力差不多的时候，运气就发挥作用了。看下面的图片。如果C罗和C罗带队打一场比赛，谁胜谁负还不确定。

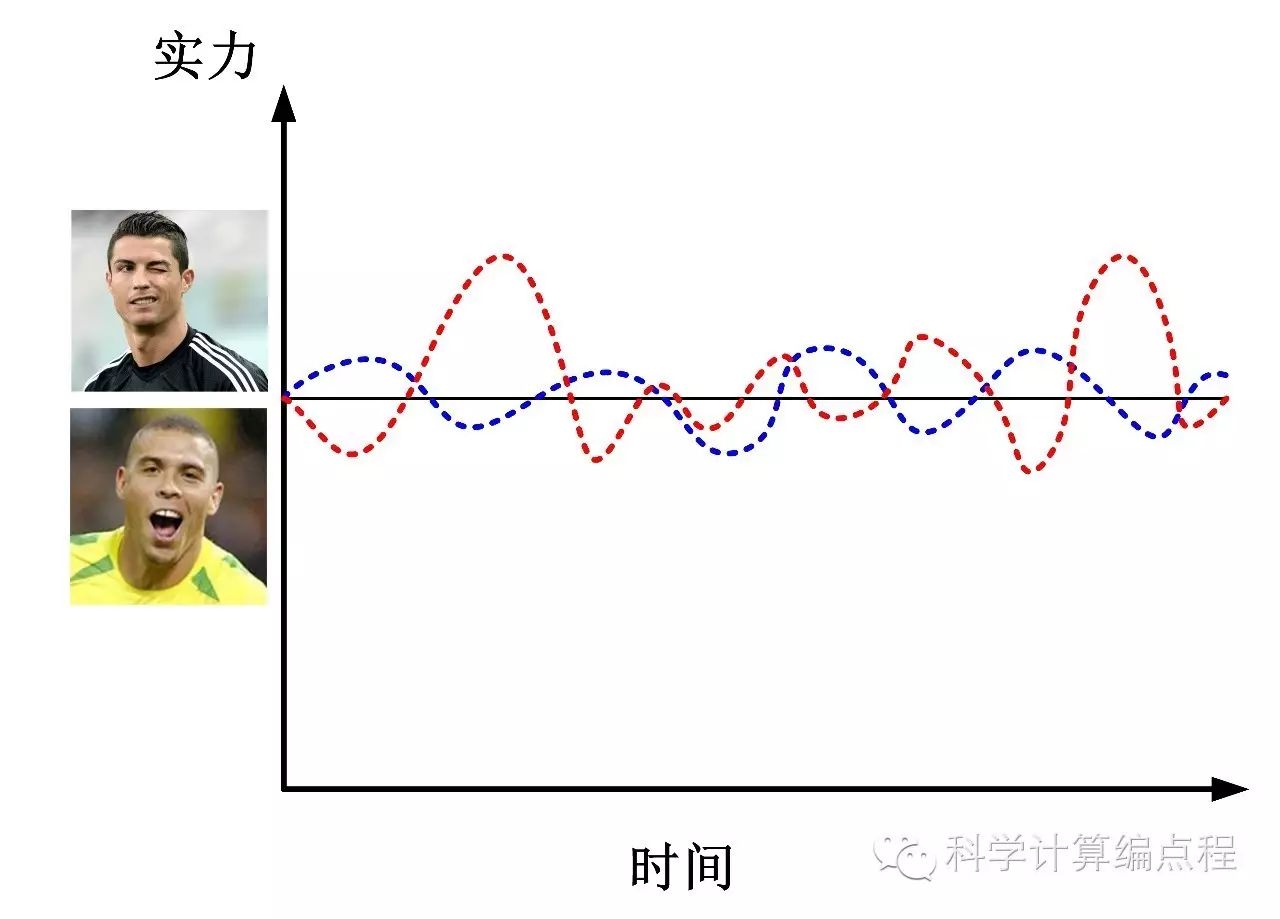
由于场上的实际表现=绝对实力+运气，所以在一场足球比赛中，如果能够分别计算两队的绝对实力和运气，就可以得到他们的实际表现得分。通过比较这个分数，您可以预测哪支球队更有可能获胜。

现在问题的关键就变成了：如何量化绝对实力和运气成分。

2. 绝对实力的量化

一支球队的实力取决于其比赛历史。这里我们根据小组赛阶段的技术参数来评估各队的实力。

2.1 小组赛参数

欧洲杯官网有很多技术参数，包括所有比赛的总体参数，比如

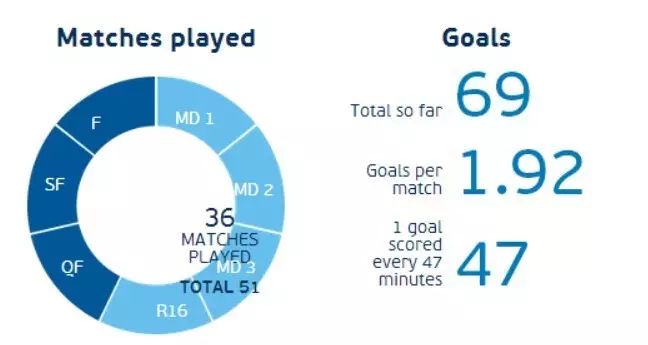
小组赛共进行36场比赛，共打进69球，场均进球1.92个。

再比如，最容易进球的时间发生在下半场开始时（第46至60分钟），然后是上半场和下半场结束时（第31至45分钟、76至90分钟）。

值得一提的是，最后补时阶段（90+），哪怕只有几分钟，也是进球的高峰期。这张图解释了为什么在裁判哨声响起之前判断足球比赛的结果并不重要。

官网还有各队详细的技术参数，如进球数、射门数、投篮命中率、角球、控球、成功传球、抢断、犯规、越位和失球等。

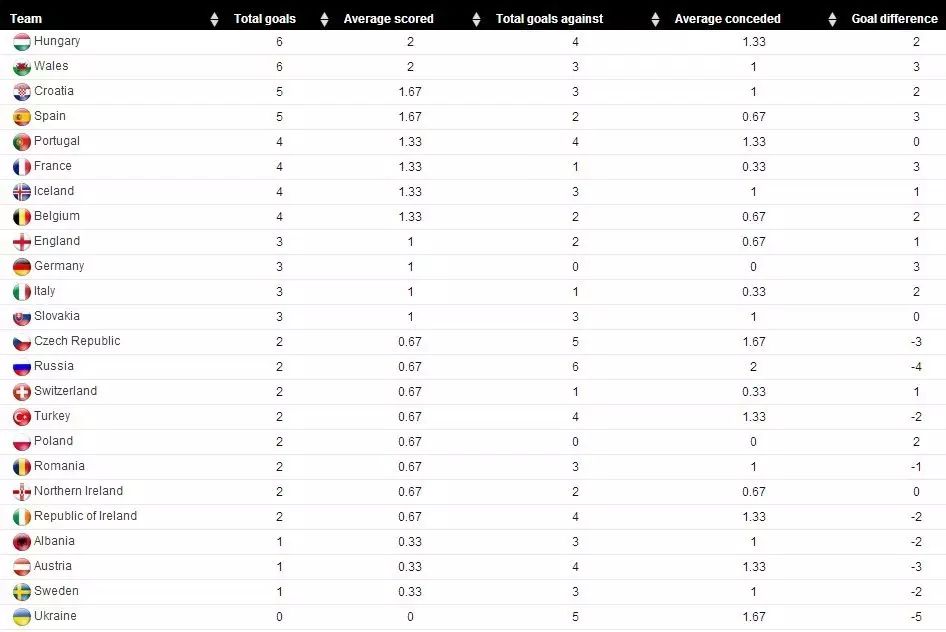
我们在表中列出这些参数：

2.2 主成分分析

上表中有这么多的技术参数，哪一个或哪些参​​数最适合评价团队的整体实力呢？另外，很多参数还是相关的。例如，小组赛积分与进球数和失球数密切相关，并且参数之间相互干扰。

因此，需要找到一种合理的方法，在减少需要分析的参数的同时，尽量减少原始技术参数所包含信息的损失，从而达到对所有参数进行综合分析的目的。

主成分分析法是这样一种方法：尝试用一组不相关的综合变量（原技术参数的线性组合）代替原来的技术指标，同时从中尽可能多地选择一个或几个综合变量尽量根据实际需要。更多信息反映了原始技术指标。然后通过少量综合变量的分析来解决问题。

主成分分析的一般步骤为：

(1)计算相关系数矩阵

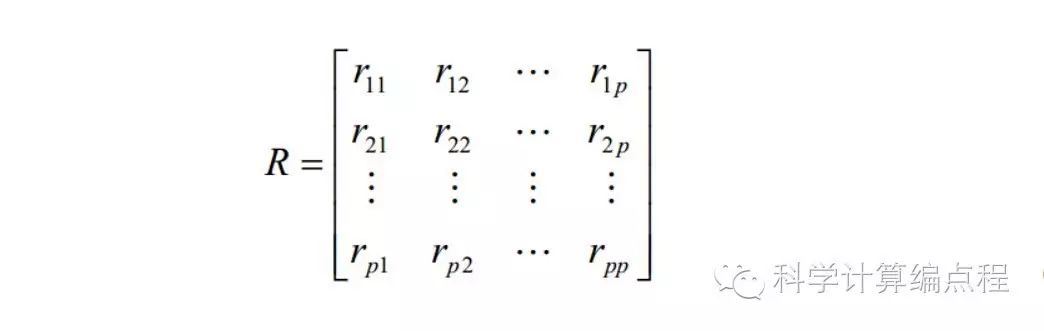
式中，rij(i,j=1,2,…,p)为原变量xi与xj之间的相关系数，其计算公式为：

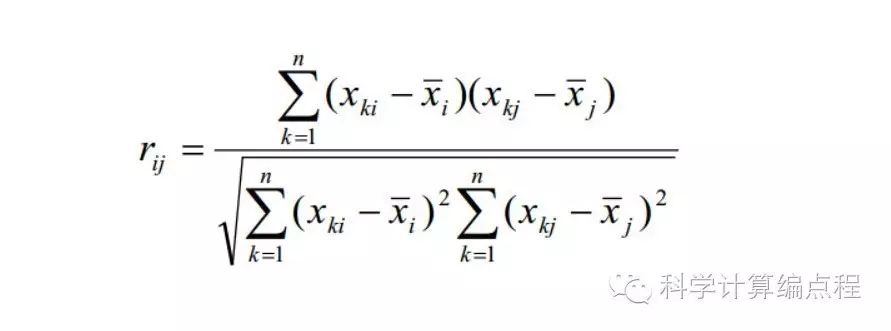
(2)计算特征值和特征向量

求解特征方程 |λI − R| = 0，然后分别求出特征值 λi 对应的特征向量 ei (i=1, 2,…,p)。

(3)计算主成分贡献率和累计贡献率

贡献率是数据各维度对整个数据的区分度的贡献。贡献率最大的是主成分，贡献率第二大的是次主成分。主成分zi的贡献率为

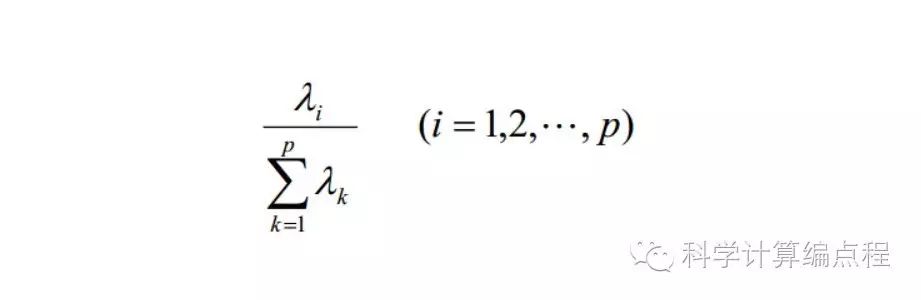
累计贡献率为

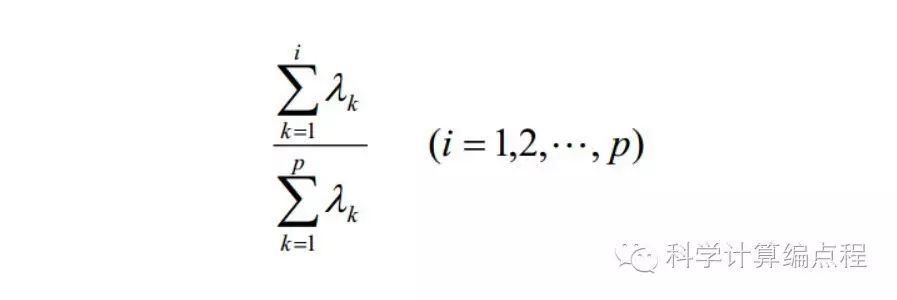
Matlab中有现成的主成分分析函数princomp。使用方法如下：

[coef,分数,方差,t2] = princomp(x)

x：为要输入的n维原始数据矩阵。

Score：生成的n维处理数据存储在score中。它是对原始数据进行分析，然后将得到的数据放在新的坐标系中。

方差：是特征值，按贡献率从大到小排列）。

coef：是系数矩阵。

2.3 实力一览表

将欧洲杯小组赛的技术参数带入该函数，可以计算出各组成部分的特征值和贡献率：

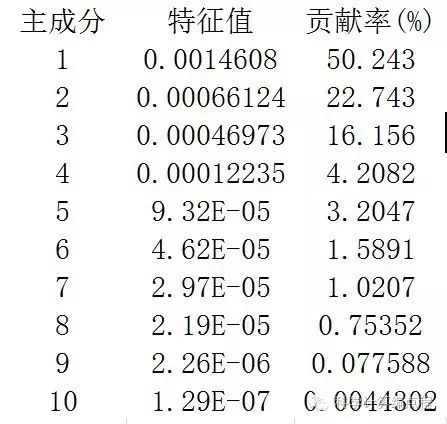
和主成分的特征值向量：

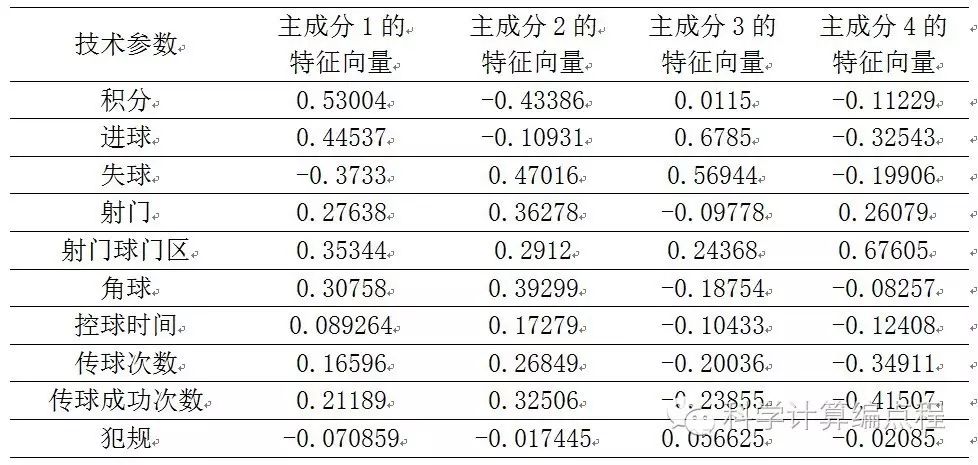
可以看出，第一主成分的贡献率远大于其他主成分，说明第一主成分能够反映大部分信息。

再看第一主成分的特征向量，各个变量所占的比例大致相等，说明第一主成分是所有技术指标的综合衡量指标。

此外，它与球队的得分、进球数、射门次数、射正率密切相关，与失球数和犯规数成反比关系，更能反映实际情况。

因此，可以根据第一主成分的特征向量对原始技术指标进行变换，求和即可得到团队实力排名。

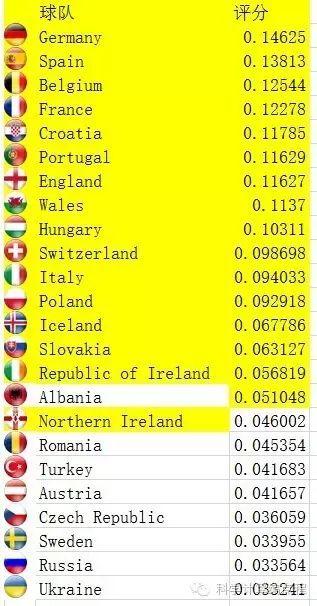
上表是利用主成分分析对小组赛数据进行分析后得出的各队实力得分。德国队最强，其次是西班牙队，其次是比利时队和法国队。球队实力与最终16强入围选手不相上下。

3. 运气因素的量化

场上实际表现=绝对实力+运气

上面已经量化了各队的绝对实力，下面将量化运气成分。

当两队比赛时，假设：

运气=两队绝对实力差的绝对值*随机因子*权重

即反映运气的参数有3个：

（1）运气对一支球队最终成绩的影响大小与两支球队的绝对实力差异大致在同一数量级。

(2) 随机因子，设置为-1到1之间的随机数。

(3)权重系数，即运气与绝对实力的比例，分别选择权重系数0.5、0.75、1、1.25、1.5进行测试。

程序源代码如下，包括主程序和匹配结果函数comparematch。

比赛结果函数comparematch可以预测单场比赛。步骤是首先根据各队的实力和运气计算出场上表现，然后比较两队的场上表现，得到单场比赛的结果。

函数 winp=comparematch(玩家1,玩家2,体重)

斯科=[

10.14625% 德国

20.13813% 西班牙

30.12544% 比利时

40.12278%法国

50.11785% 克罗地亚

60.11629% 葡萄牙

70.11627% 英格兰

80.1137% 威尔士

90.10311% 匈牙利

100.098698% 瑞士

110.094033% 意大利

120.092918% 波兰

130.067786% 冰岛

140.063127% 斯洛伐克

150.056819% 爱尔兰共和国

160.046002% 北爱尔兰

];

sco1=sco(玩家1,2);

sco2=sco(玩家2,2);

增量=绝对值(sco1-sco2);

兰特因子1=兰特()*2-1;

realsco1=sco1+deltas*randfactor1*权重；

兰特因子2=兰特()*2-1;

realsco2=sco2+deltas*randfactor2*权重；

如果realsco1>realsco2

winp=玩家1；

别的

winp=玩家2；

结尾

主函数模拟了总共10万次的淘汰赛过程。每次模拟都会调用比赛结果函数给出单场比赛的结果，进而得到淘汰赛的结果。最后，统计所有结果：

清除

CLC

模拟时间=1:100000

% 1/8 最终

最终8队=[

10 12

5 6

8 16

9 3

1 14

11 2

4 15

7 13

];

权重=1；

对于我=1:8

玩家1=Final8team(i,1);

玩家2=Final8team(i,2);

Final4team(ceil(i/2-0.1),2-mod(i,2))=...

比较匹配（玩家1，玩家2，体重）；

结尾

% 1/4 最终

重量=重量+0.1；

对于我=1:4

玩家1=Final4team(i,1);

玩家2=Final4team(i,2);

Final2team(ceil(i/2-0.1),2-mod(i,2))=...

比较匹配（玩家1，玩家2，体重）；

结尾

% 1/2 最终

重量=重量+0.1；

对于我=1:2

玩家1=最终2队(i,1);

玩家2=最终2队(i,2);

Final1team(ceil(i/2-0.1),2-mod(i,2))=...

比较匹配（玩家1，玩家2，体重）；

结尾

％最终的

重量=重量+0.1；

我=1；

玩家1=最终1队(i,1);

玩家2=最终1队(i,2);

Finalwin(模拟时间)=...

比较匹配（玩家1，玩家2，体重）；

结尾

制表(Finalwin)

4.谁是冠军？

仿真统计结果如下：

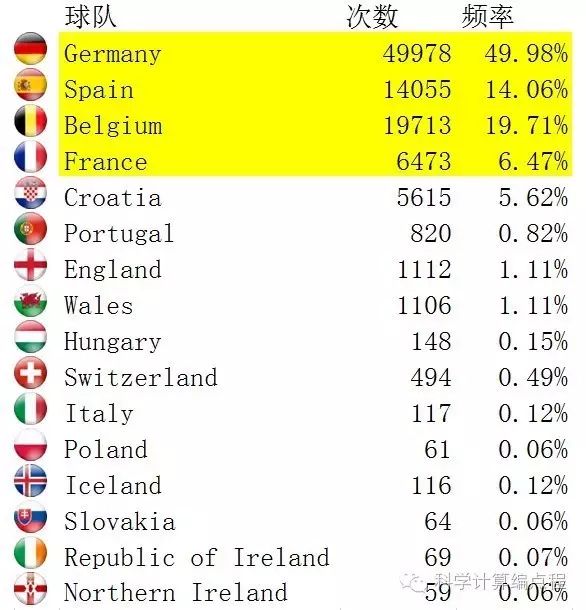
在10万次模拟中，德国队夺冠次数为49,978次，西班牙队夺冠次数为14,055次……如果画成条形图的话，那就是：

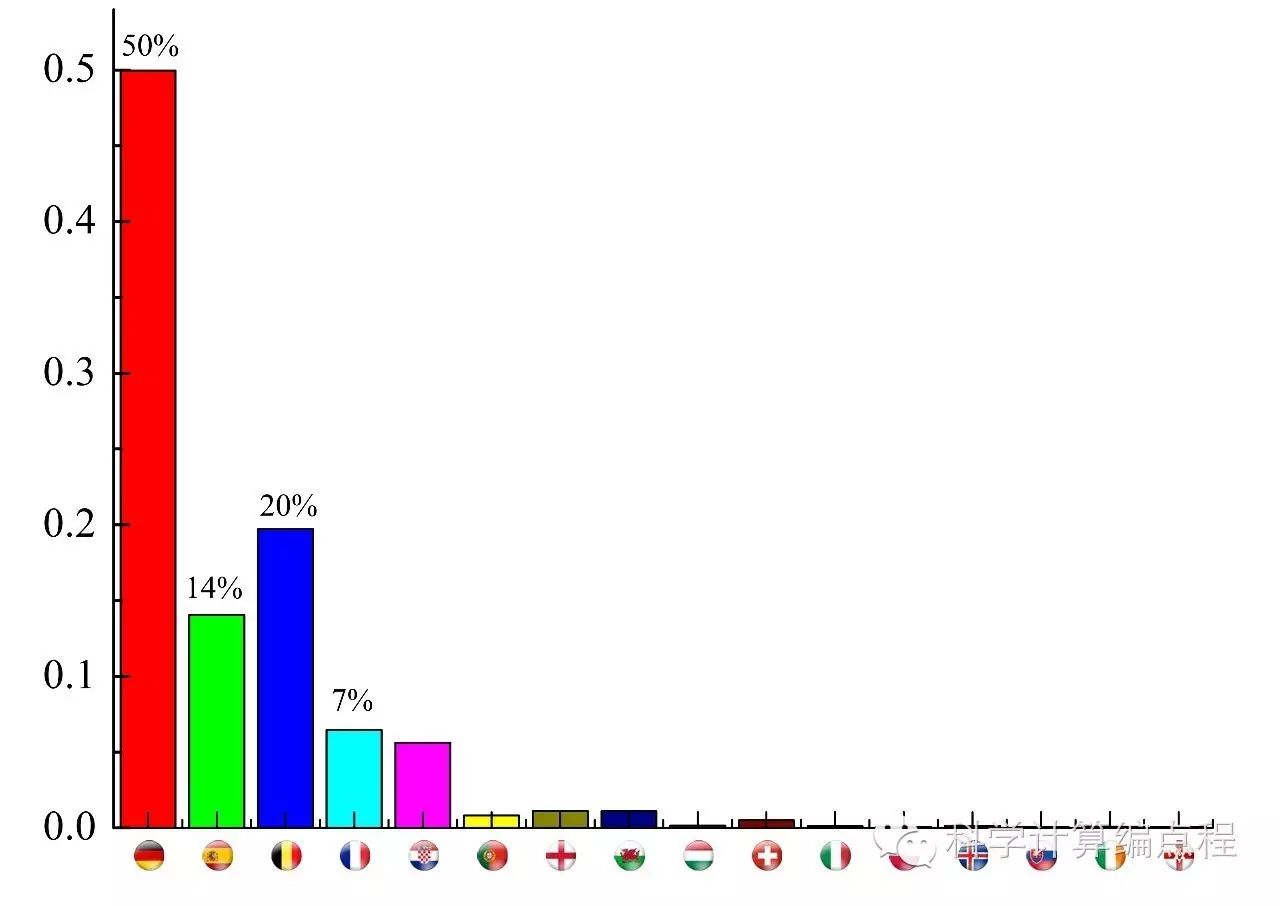
德国队、西班牙队、比利时队获胜概率最高。三队加起来获胜概率超过84%。这三支球队中，德国队获胜的概率最高。

值得一提的是，上述预测中还有一些因素没有考虑，例如：

(1)所有团队的随机影响因素不一定是均匀分布的。比如法国队是主场作战，所以运气因素可能会更高一些；

(2)以上预测是基于小组赛成绩。但每支球队的表现都敏感地取决于上场的球员。如果要做更精准的分析，就需要对每个球员的技术参数进行单独分析。这已经超出了看欧洲杯连球星都认不出来的伪球迷的认知能力……

所以，想根据上述预测购买彩票的同学们还是停下来吧。场上发生了很大的变化。购买彩票存在风险。投资时请谨慎。欧洲冠军预测仅供娱乐，我们不承担由此产生的任何法律或道德责任。

（结尾）